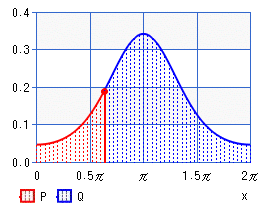
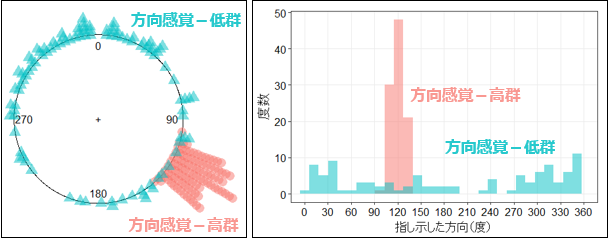
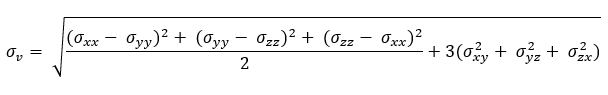フォン・ミーゼス分布

フォン・ミーゼス分布（フォン・ミーゼスぶんぷ; 英: von Mises distribution）は、円周上に定義された連続型の確率分布である。方向統計学における代表的な分布モデルであり、確率変数を角度の関数として表す分布モデルなどに使われる。名前はリヒャルト・フォン・ミーゼスに因む。

定義と性質

μ (0 ≤ μ < 2π), β (β ≥ 0) をパラメータ、実数 θ (0 ≤ θ < 2π) を確率変数とするときのフォン・ミーゼス分布の累積分布関数 F(θ) および確率密度関数 f(θ) は以下の式で定義される。

F(\theta )=\left\{2\pi I_{0}(\beta )\right\}^{-1}\left[\theta I_{0}(\beta ) 2\left\{\sum _{j=0}^{\infty }{\frac {I_{j}(\beta )\sin(j(\theta -\mu ))}{j}}\right\}\right]

f(\theta )={\frac {\exp\{\beta \cos(\theta -\mu )\}}{2\pi I_{0}(\beta )}}

ここで

I_{j}(\beta )=\left({\frac {\beta }{2}}\right)^{j}\sum _{i=0}^{\infty }{\frac {\left({\frac {\beta ^{2}}{4}}\right)^{i}}{i!\Gamma (j i 1)}}

は j 次の第一種変形ベッセル関数である。パラメータ β が大きいとき正規分布に近似でき、β = 0 のとき一様分布に帰着する。

定義域が有限 (0 ≤ θ < 2π)、または θ に関して周期関数であることから、正規分布とは異なるが、方向統計学における代表的な分布であること、二変量正規分布を変換することでフォン・ミーゼス分布を得られること、最尤推定により平均方向が得られることなど、正規分布と類似性もあることから、円周正規分布 (circular normal distribution) と呼ばれることもある。しかし、再生性を持たない等、正規分布と異なる性質もある。